失控的系统和生成艺术
在失控的系统中,利用简单规则涌现出复杂的艺术形态
我们先看一个著名的基于计算的生命游戏——元胞自动机(又叫细胞自动机)。
假设在一个二维空间里有一种细胞生物,它的存活状态取决于它周围细胞的存活状态。

我们制定一个简单的规则:当这个细胞周围有1个或者2个细胞的时候,它就能存活(假设该位置原本没有细胞生物,则会在该位置分裂诞生新细胞);假设周围少于1个活细胞或多于2个细胞,那么它就会因孤独或者资源竞争激烈而死去。
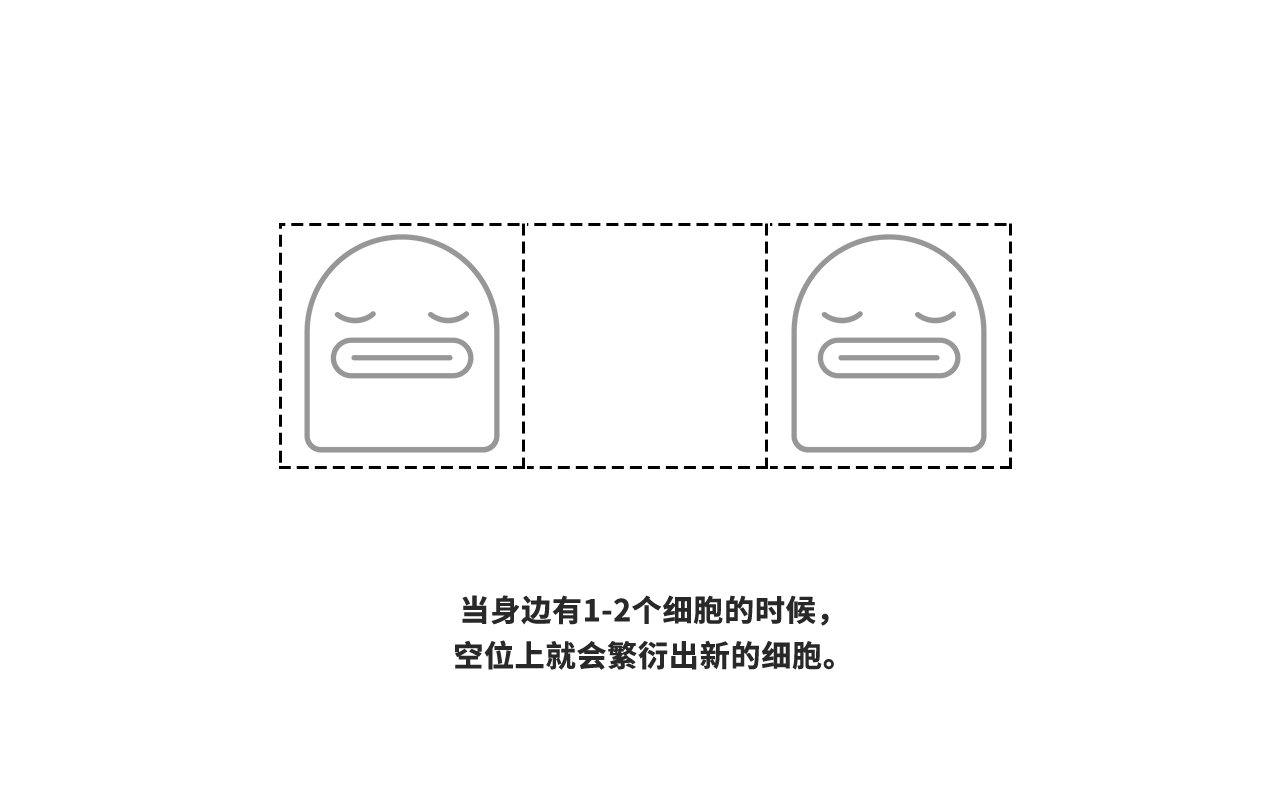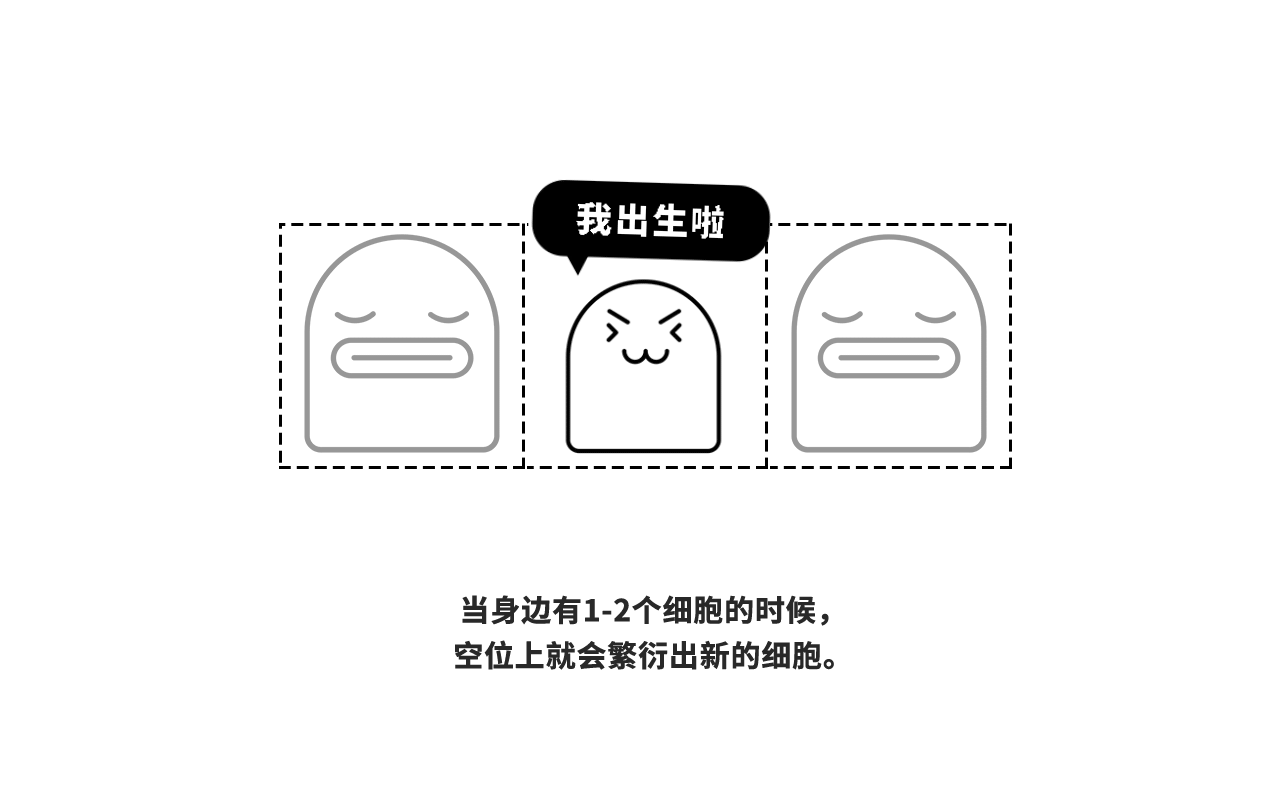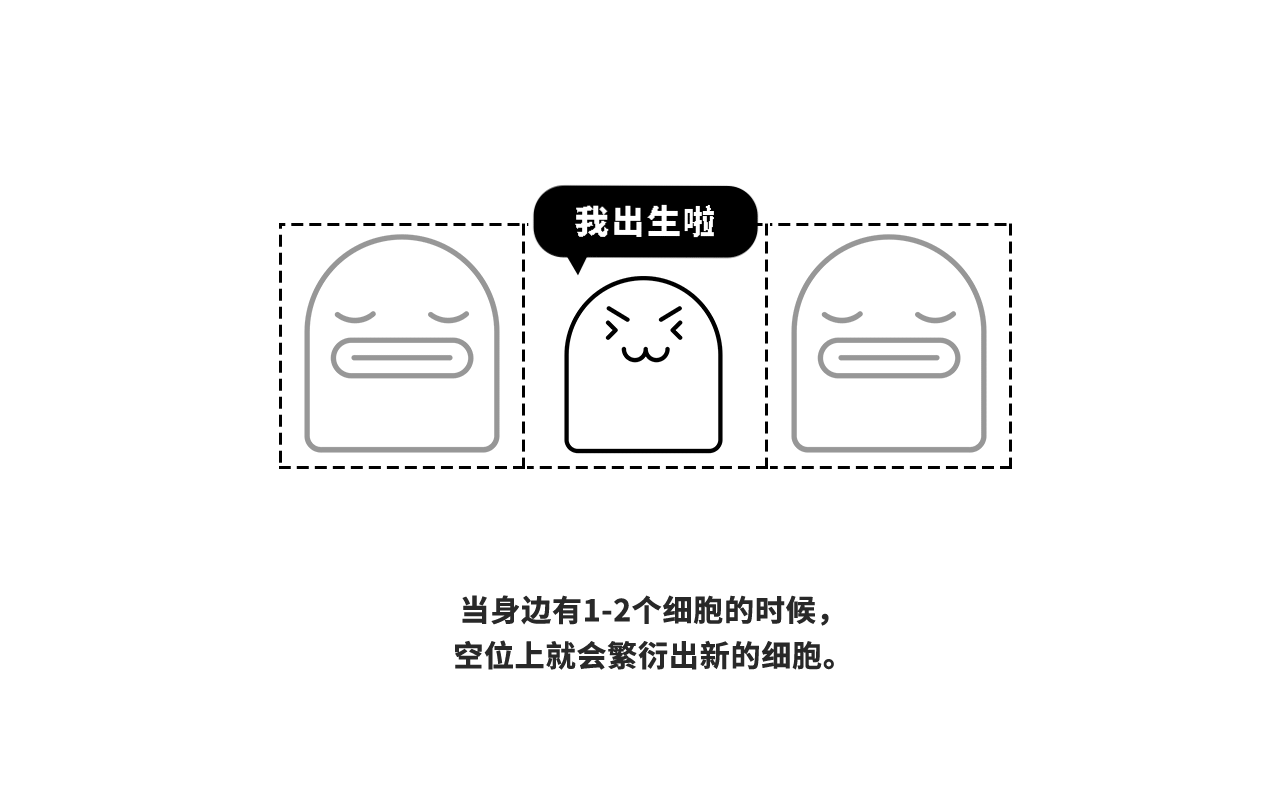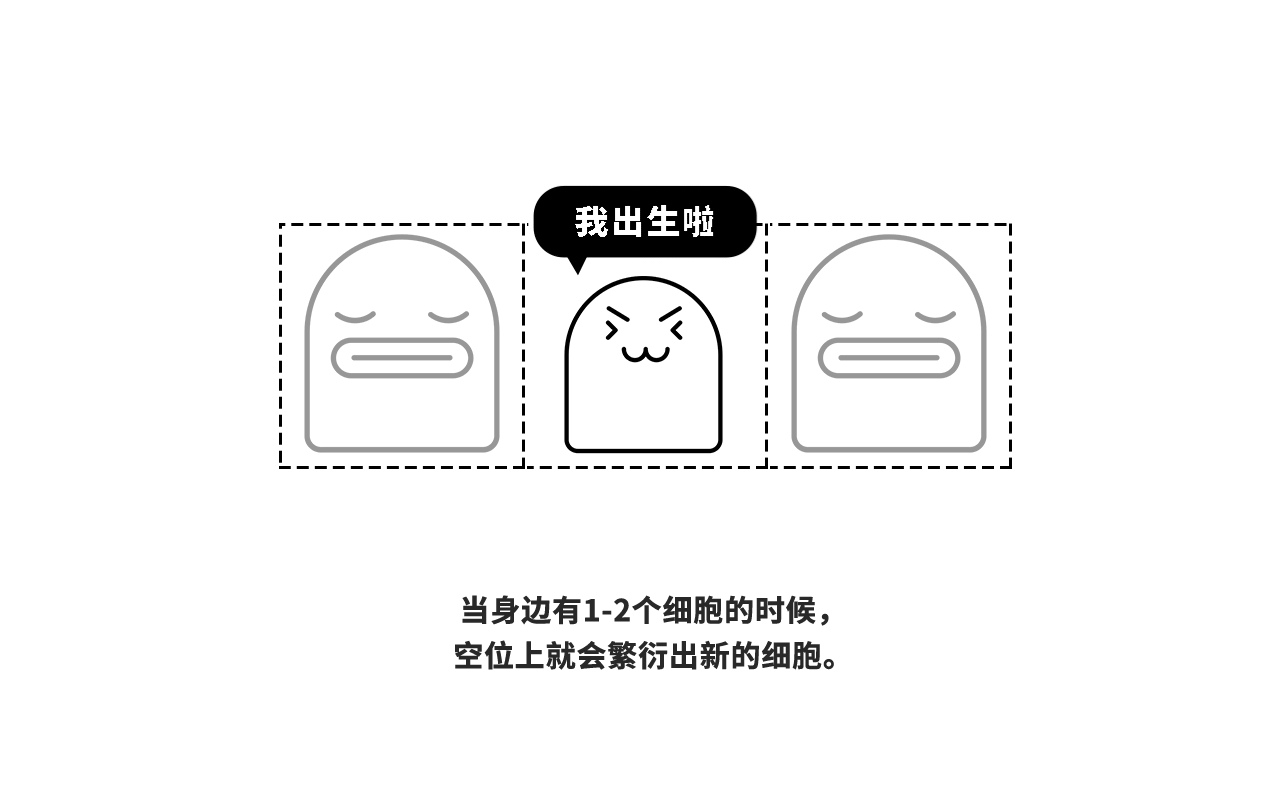


我们用计算机模拟基于以上规则的生命游戏。一开始画布是白色的,表示这个二维空间还没有细胞生物的存在。当我们在空间中心点投入第一个细胞之后,基于前面介绍的简单规则,这个二维空间会迅速演变成一个复杂且动态变化的细胞世界。

元胞自动机由冯·诺依曼在上世纪50年代的时候提出,但是在很长一段时间里,人们都不明白这一个规则如此简单的小游戏有什么研究意义。正是这么一个不起眼的东西,从80年代开始,就深深吸引了史蒂芬·沃尔夫勒姆这个天才,他深入地研究了初等元胞机256种规则所产生的模型,并从中收到启发。在后来接受采访的时候,史蒂芬·沃尔夫勒姆说道:
“Rule 30(256种初等元胞自动机规则之一)让我意识到,在计算的宇宙中凭借简单规则可以出现一些非常复杂的现象。”

RULE 30 生成的复杂图形
同样是和细胞有关,Andy Lomas的《Cellular Forms: an Artistic Exploration of Morphogenesis》中提出了一种生成大自然中物体复杂外形的一种方法。和其他直截了当从物体外形入手的设计方法截然相反,Andy Lomas从最简单最原始的细胞开始,给细胞设计简单的生长和运动规则,然后放手让细胞在不断繁衍生长中自下而上地生成复杂的有机形态。


上面的有机物形态都是通过Andy Lomas设计的简单规则所产生的。每个有机物形态都是从最原始的几个细胞开始,基于简单的生长和运动规则,经过数千次迭代,最终由数千万个细胞所构成。
这种现象被称为“涌现”,即基于简单规则相互作用的个体所组成的群体,可能会涌现出意料之外的更复杂、更高级的生命特征(群态)。
凯文·凯利在《失控》这本书里举了一个鸟群的例子。他这么描述道:“飞行途中的一只鸟对自己的鸟群形态并没有全局的概念。结对飞行的鸟儿对鸟群的飞翔姿势和聚合是视而不见的。‘’群态’正是从这样一群完全罔顾其群体形态、大小或列队的生物中涌现出来的。”
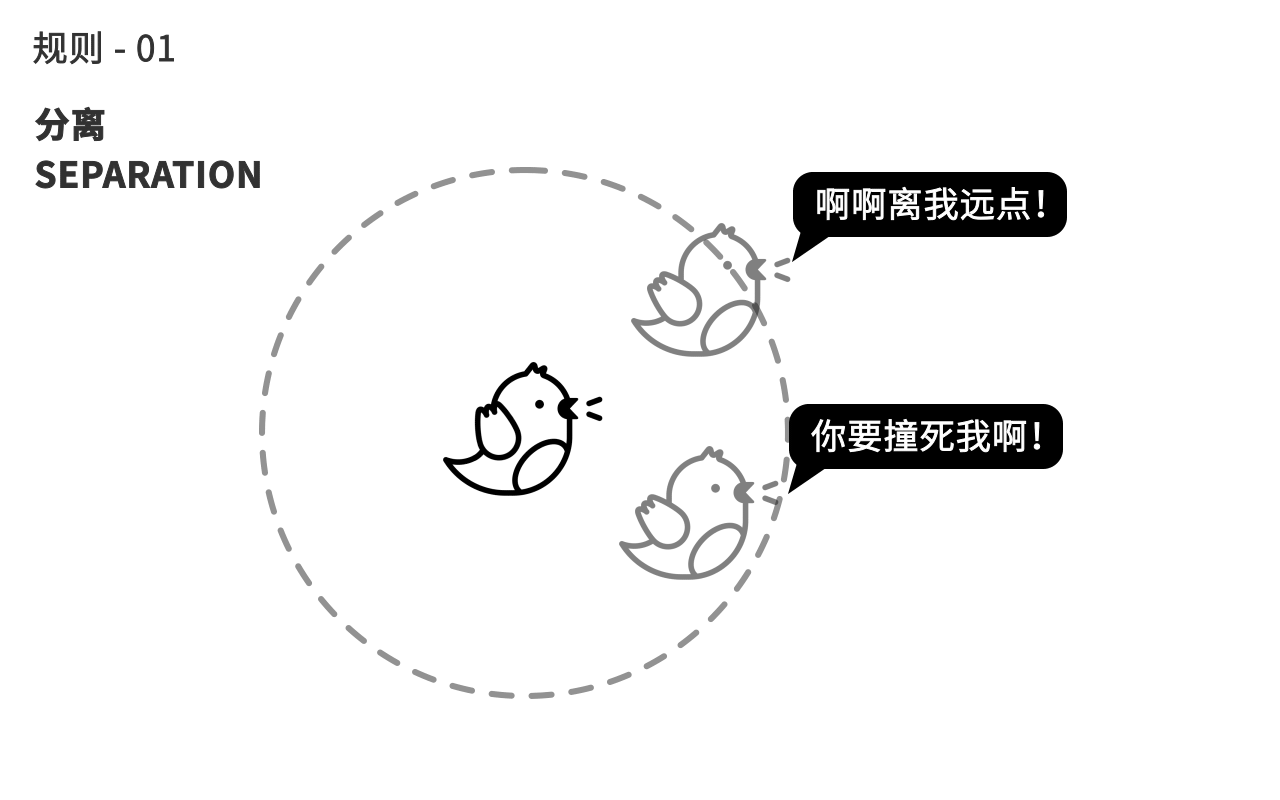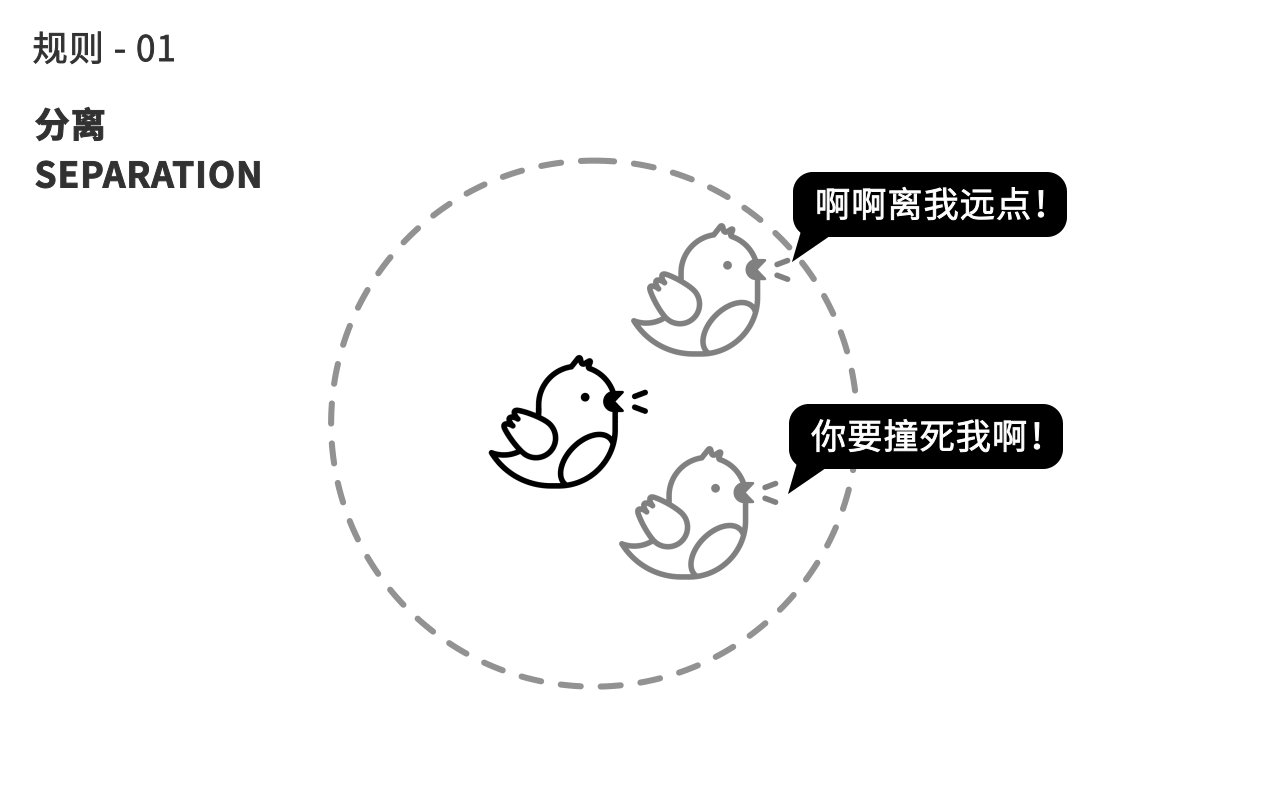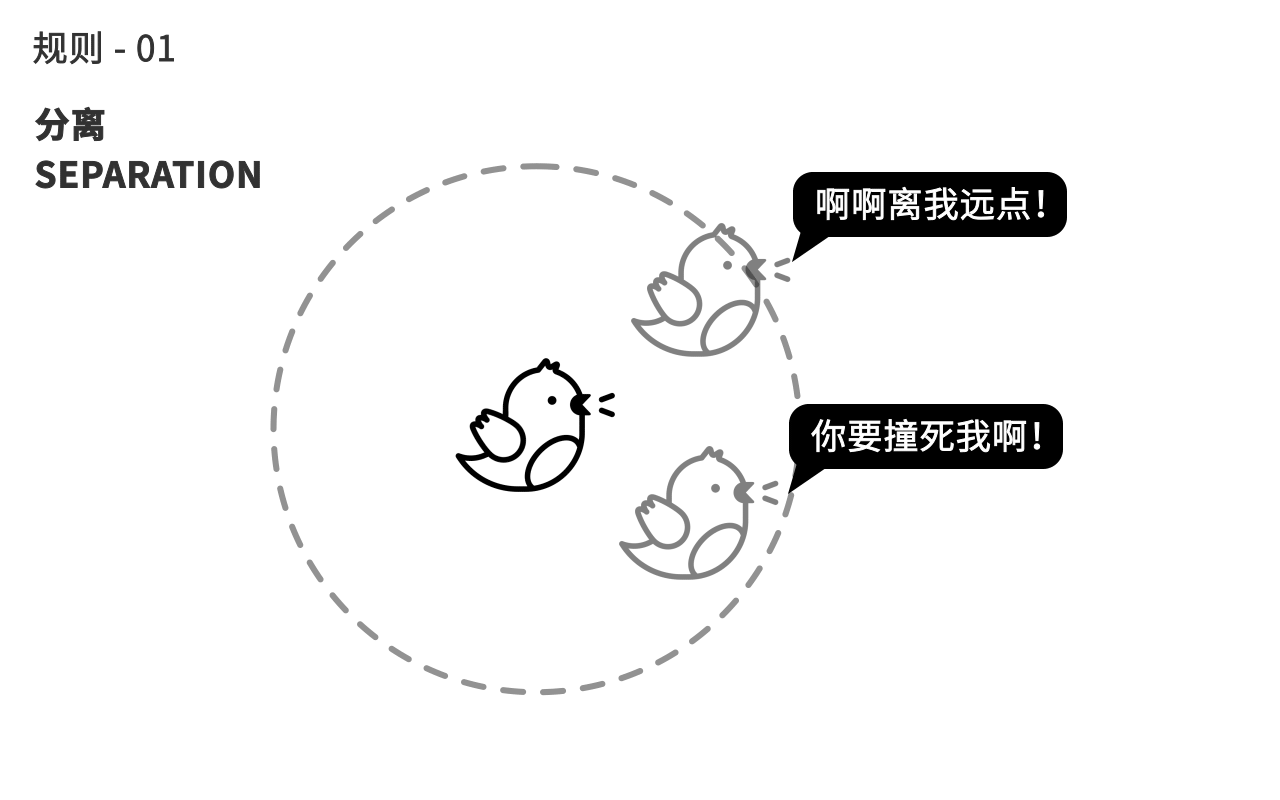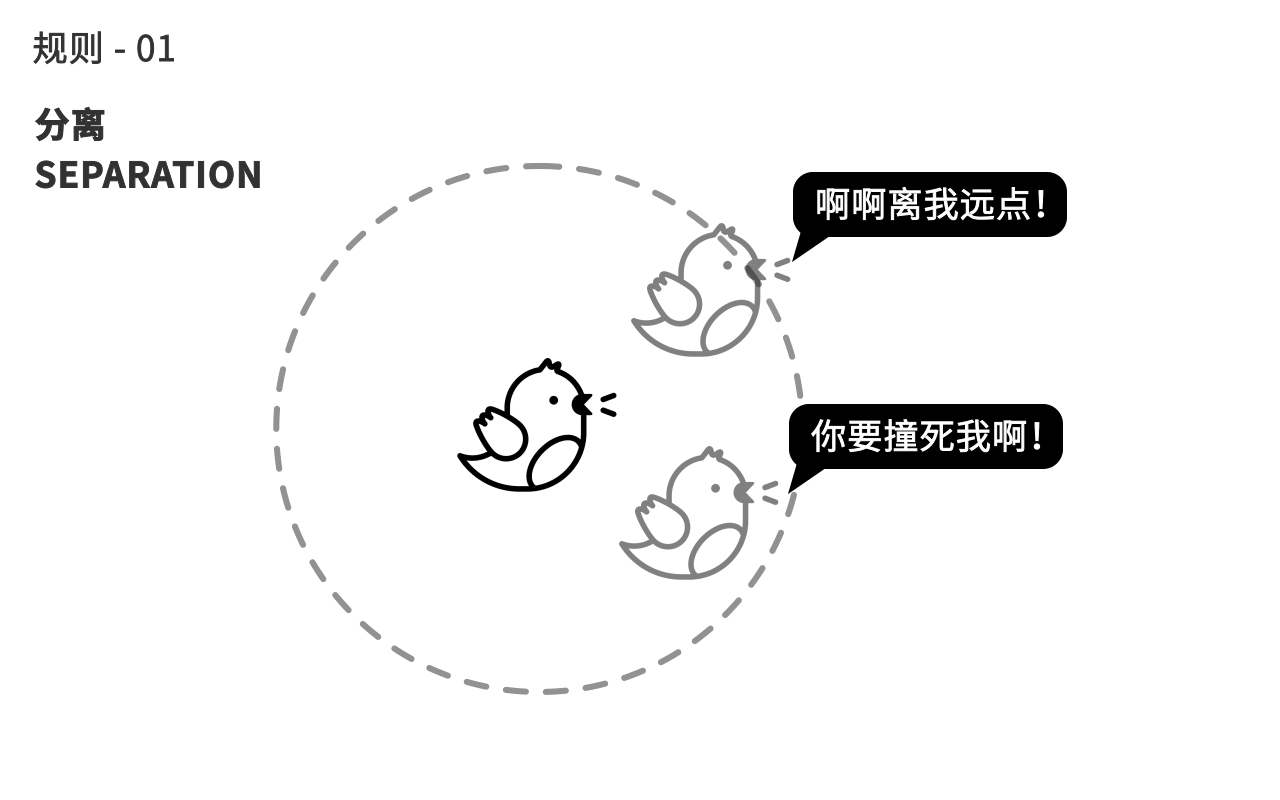
鸟鱼等动物的集群运动对熟悉编程创作的人来说并不陌生,Craig Reynolds在1986年设计的Boids 算法就是用来模拟这种群体智能的经典例子。在Boids 算法里,鸟和鸟之间的相互作用规则很简单,概括起来就三个词:分离、对齐、聚拢。
第一个规则,这只鸟会和身边的同伴保持一定距离,避免撞机,当同伴太靠近自己的时候,鸟会往反方向移动。
第二个规则,鸟会自动调整自己的朝向,来趋向和身边同伴的平均朝向。
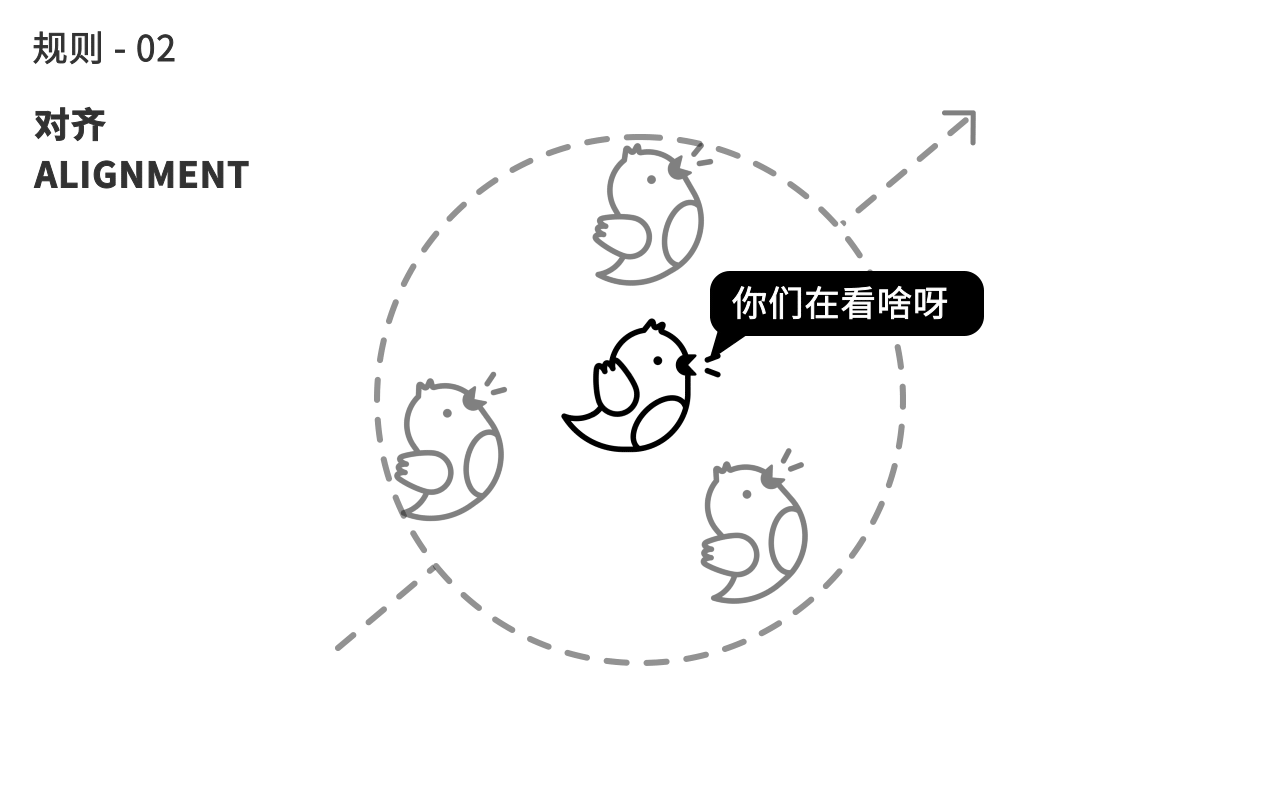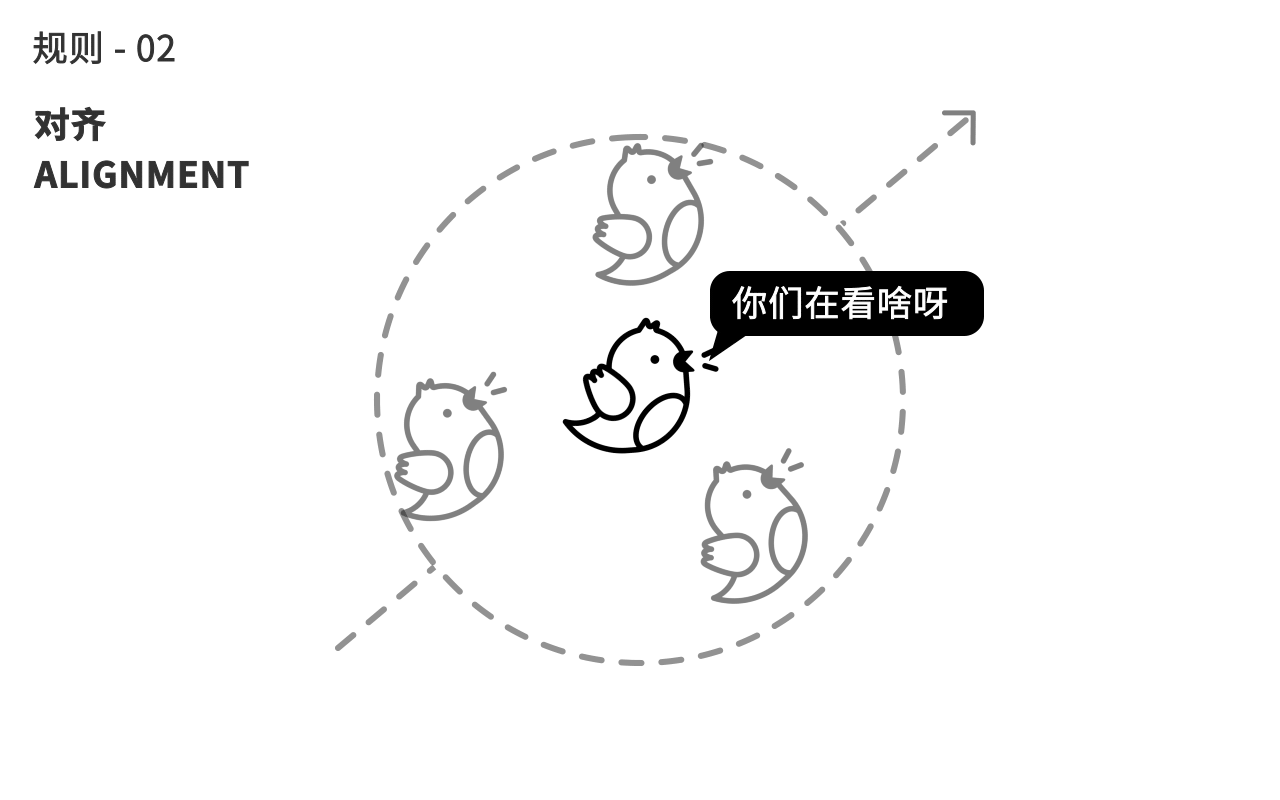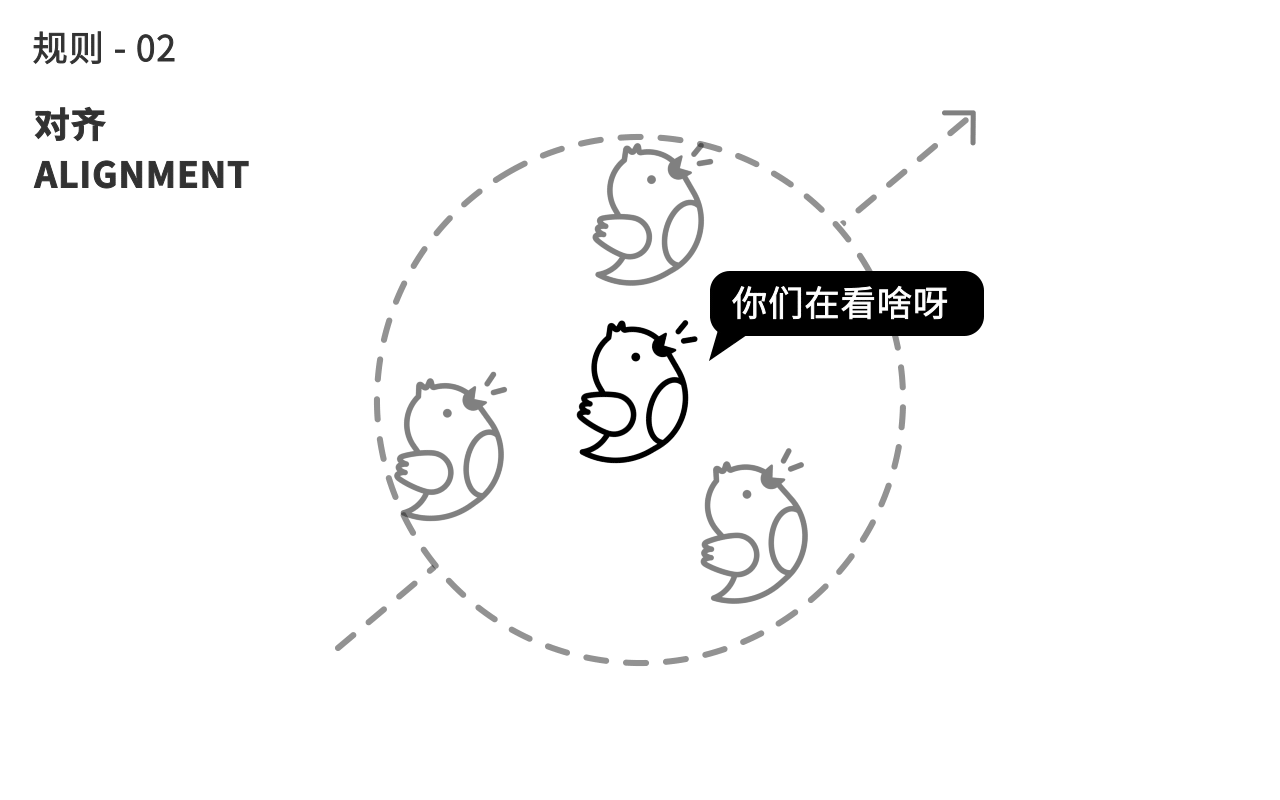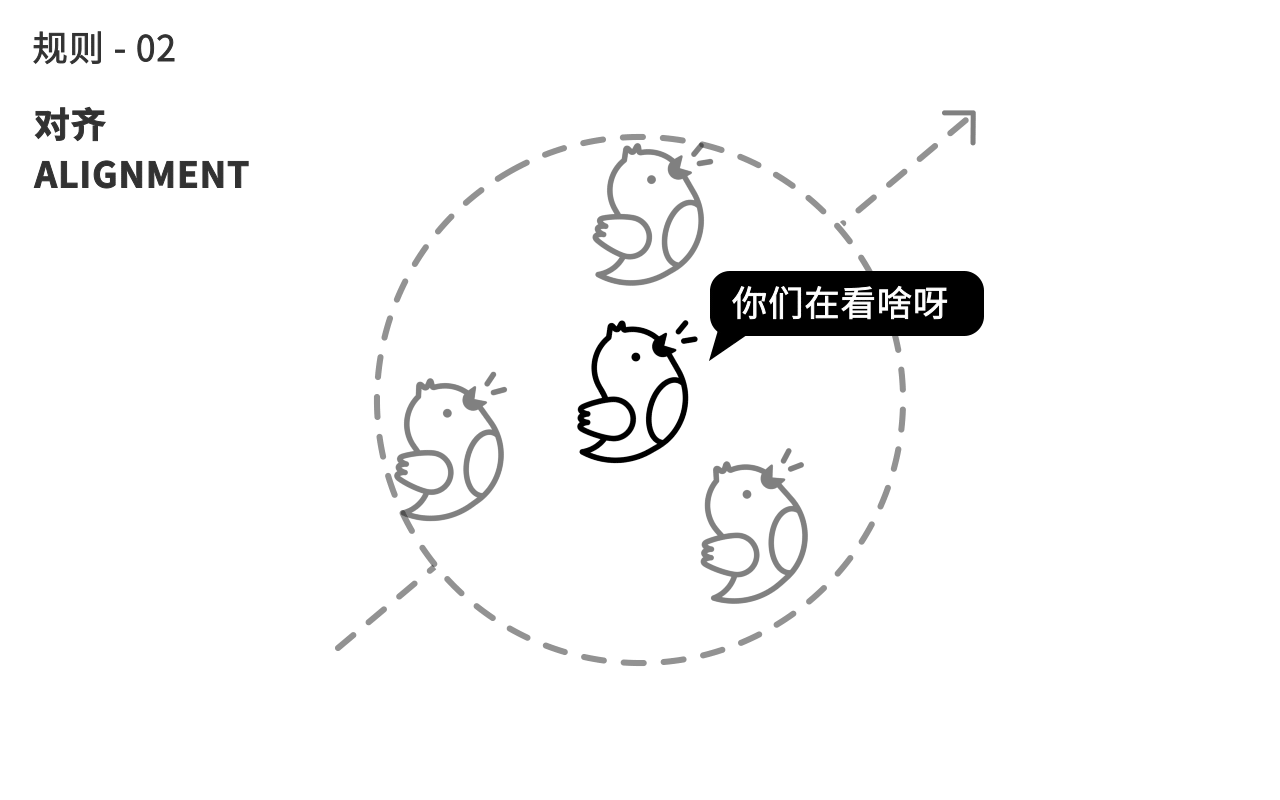
第三个规则,鸟会计算周围同伴的平均距离,来往中间聚拢,避免自己离群。
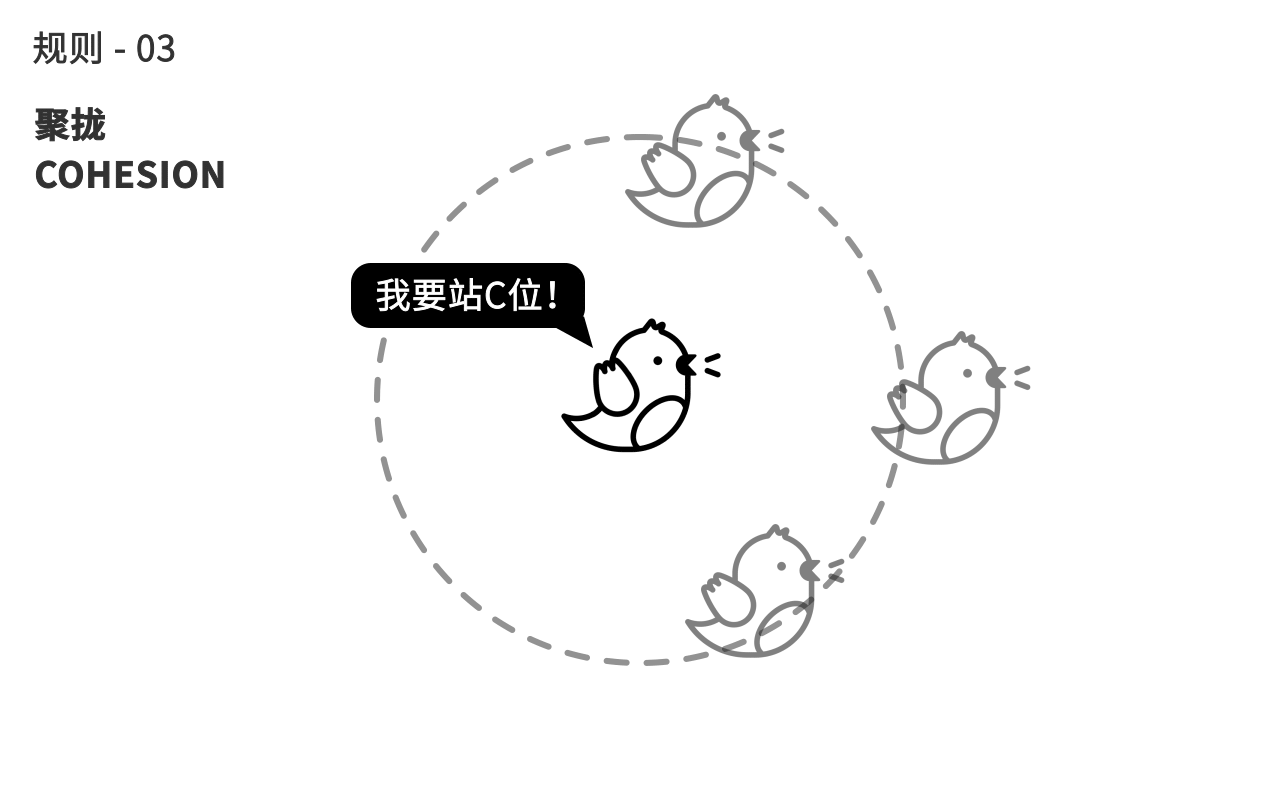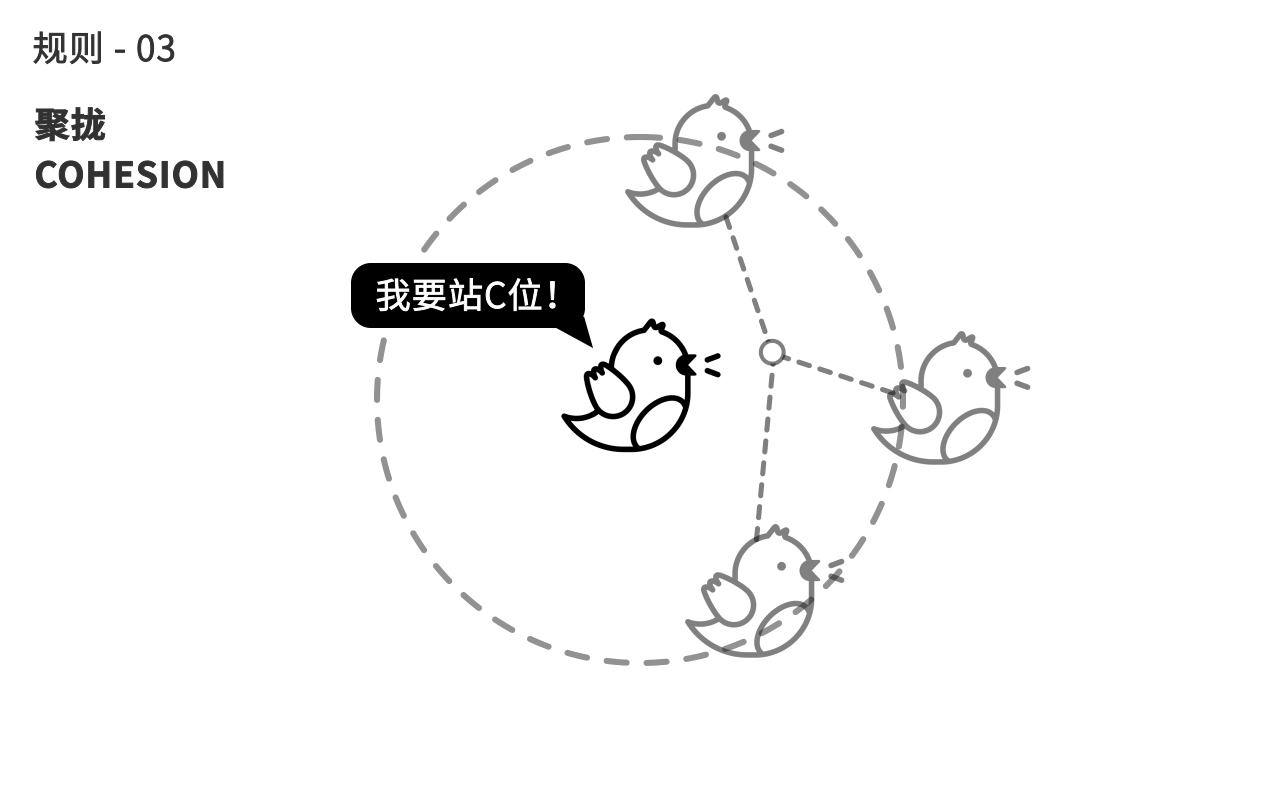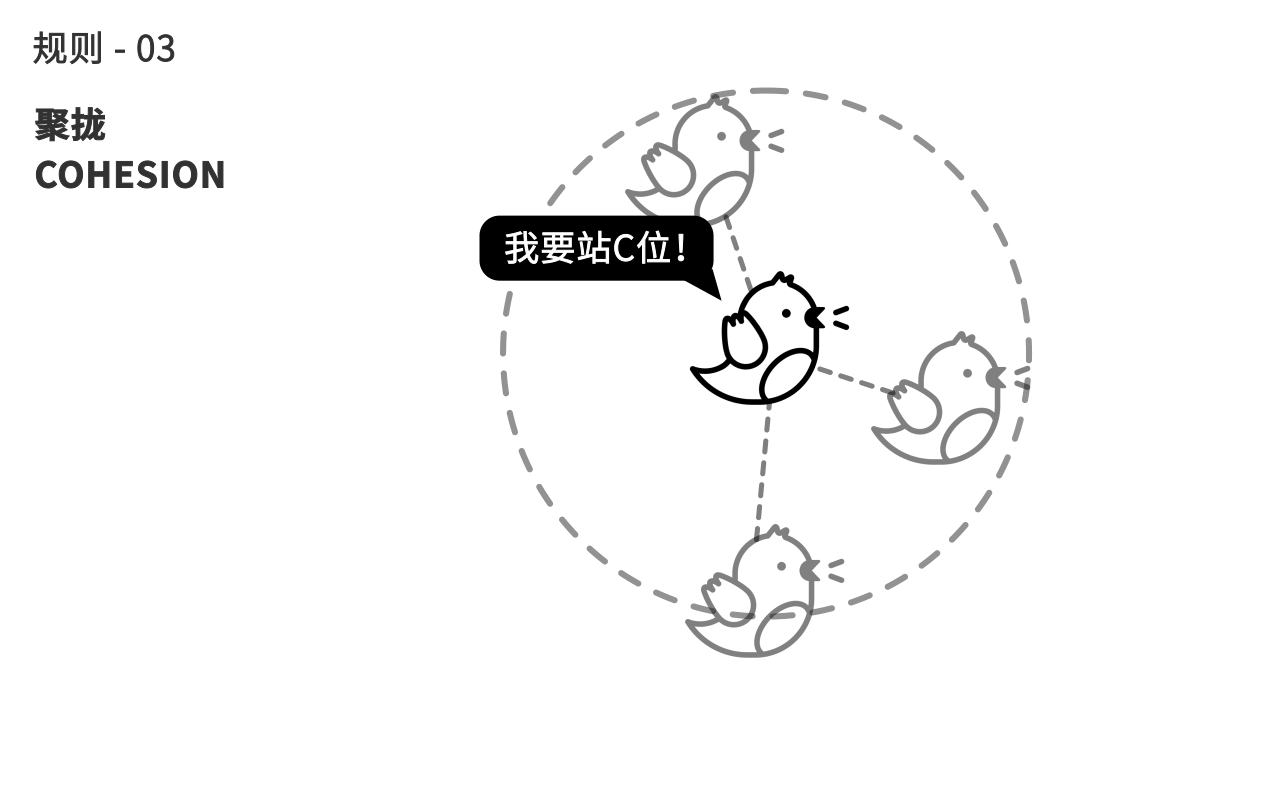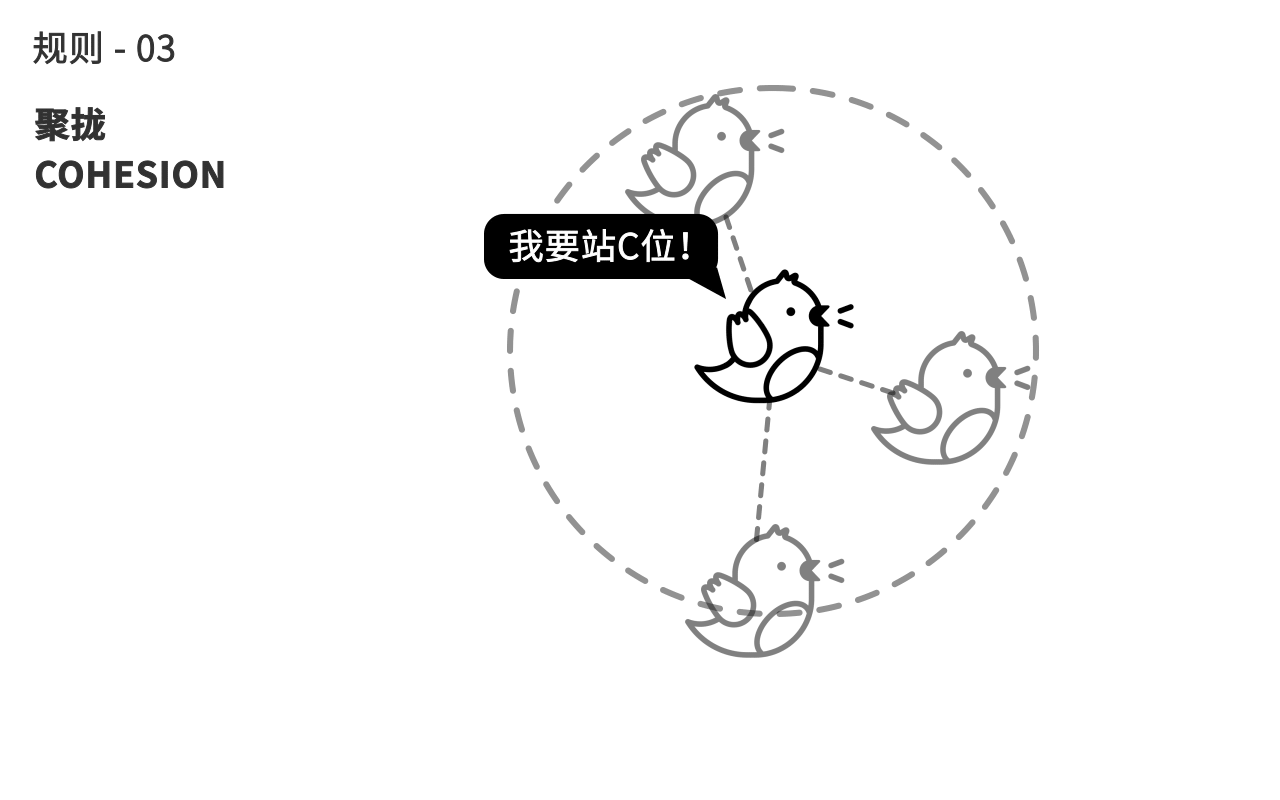
在计算机中我们基于Boids这三个简单的规则,来决定每一帧每一只小鸟个体所在的位置,而由此导致的整个鸟群的形态时而分散时而聚拢,这种奇妙的群态看起来似乎是一种新的生命体,它的生命从哪里来?正是从每个小鸟个体之间的互动中“涌现”而出。

鸟群、蚁群等群体行为的研究属于群体智能。在群体智能里有个很重要的规则是邻近原则( Proximity Principle) ,即我们要允许个体具备简单且有限的空间和时间计算的能力。在这个例子里,每只鸟都能看到在自己周围的几只同伴,并根据这些同伴的位置、朝向,来对自己的位置和朝向做出更新。
群体智能没有中心控制,应用在生成艺术里,亦是如此。
我们传统思维里,艺术创作必须是人类(艺术家)100%参与控制而产生的。但是从某种意义上来说,我们以上所举的例子里的系统,都是“失控”的。人类(艺术家)只在一开始作为一个制定规则的角色出现,而后这个系统的走向再也不直接受人类(艺术家)控制,它的控制是分布式的,它的艺术结果是个体和个体之间基于规则的互动中“涌现”出来的。
关于生成艺术的定义存在许多种说法,但是几乎所有的定义都认可2个关键特性:完全或部分脱离人类控制的自发系统,以及不可预测的艺术生成结果。这和我们前面所讲的“失控”的系统很相似,“失控”的系统随着时间发展,所呈现的更高级更复杂的群态,也是不可从个体之间简单的交互规则所能预测到的。
让我们把目光从单一生物的群体中解放出来。众所周知我们现实生活中最大的活系统,就是我们无时不刻不身在其中的地球生态系统,它是由无数种类的生物和非生物所构成。那么我们是否能在计算机里创造多于一种生物种类的活系统?答案是肯定的。
“剪刀石头布”元胞自动机是一个存在3种生物的活系统,你可以用RGB(红色绿色蓝色)表示这3种生物,这3种生物在这个系统里形成一条像“剪刀石头布”一样首尾相接的食物链:红色生物吃蓝色生物;蓝色生物吃绿色生物;绿色生物吃红色生物。
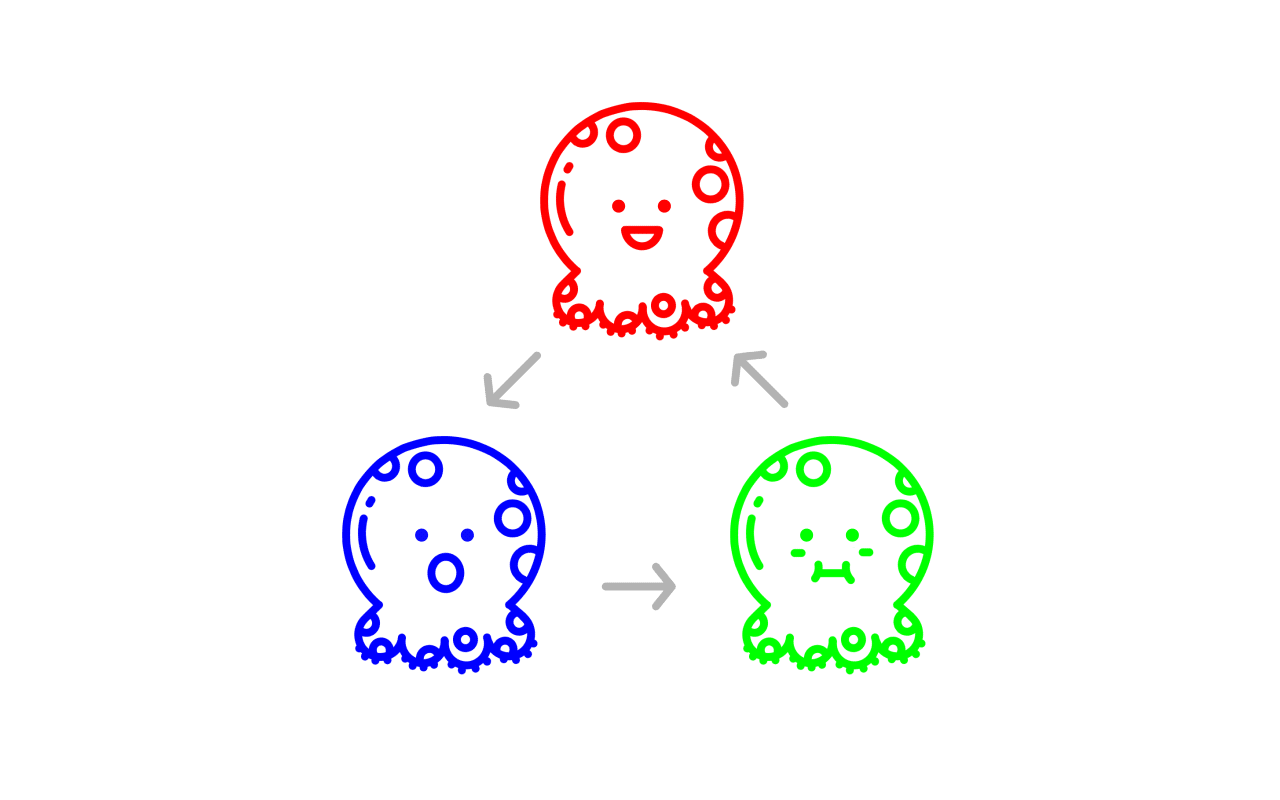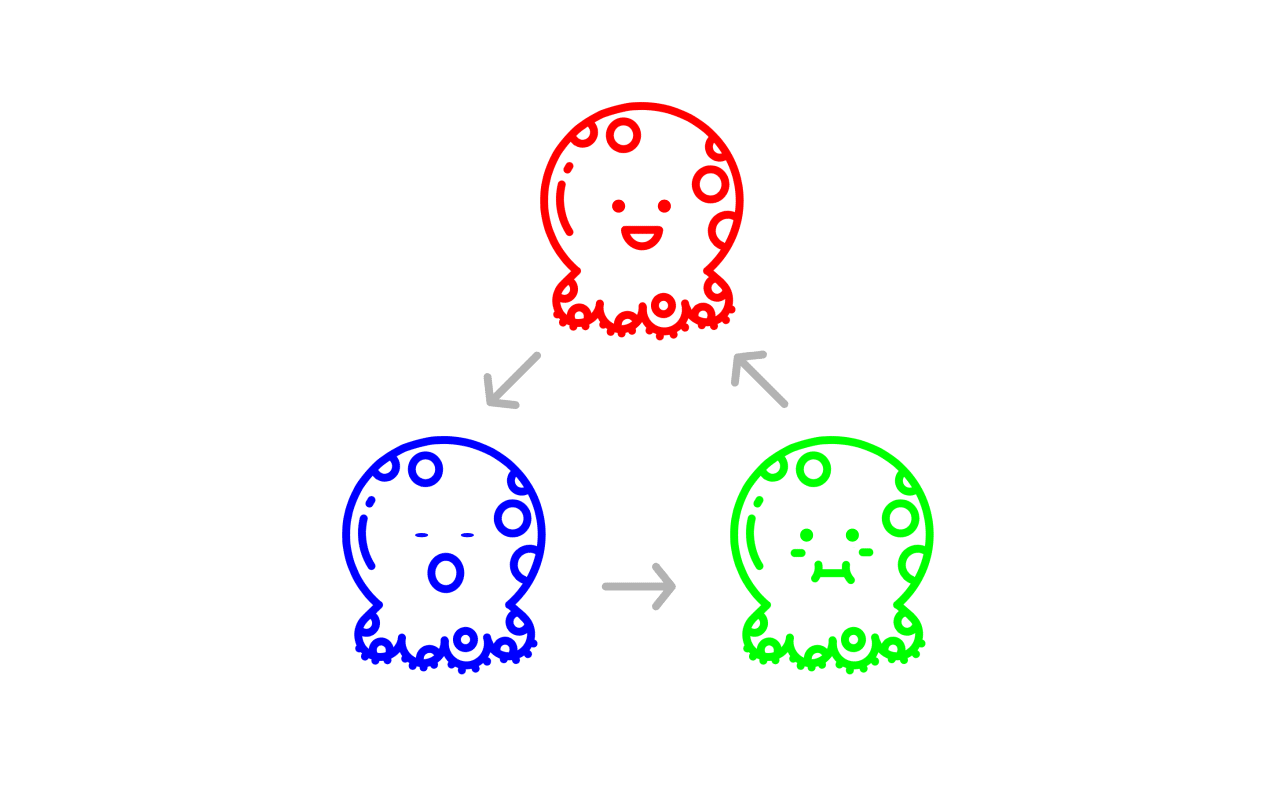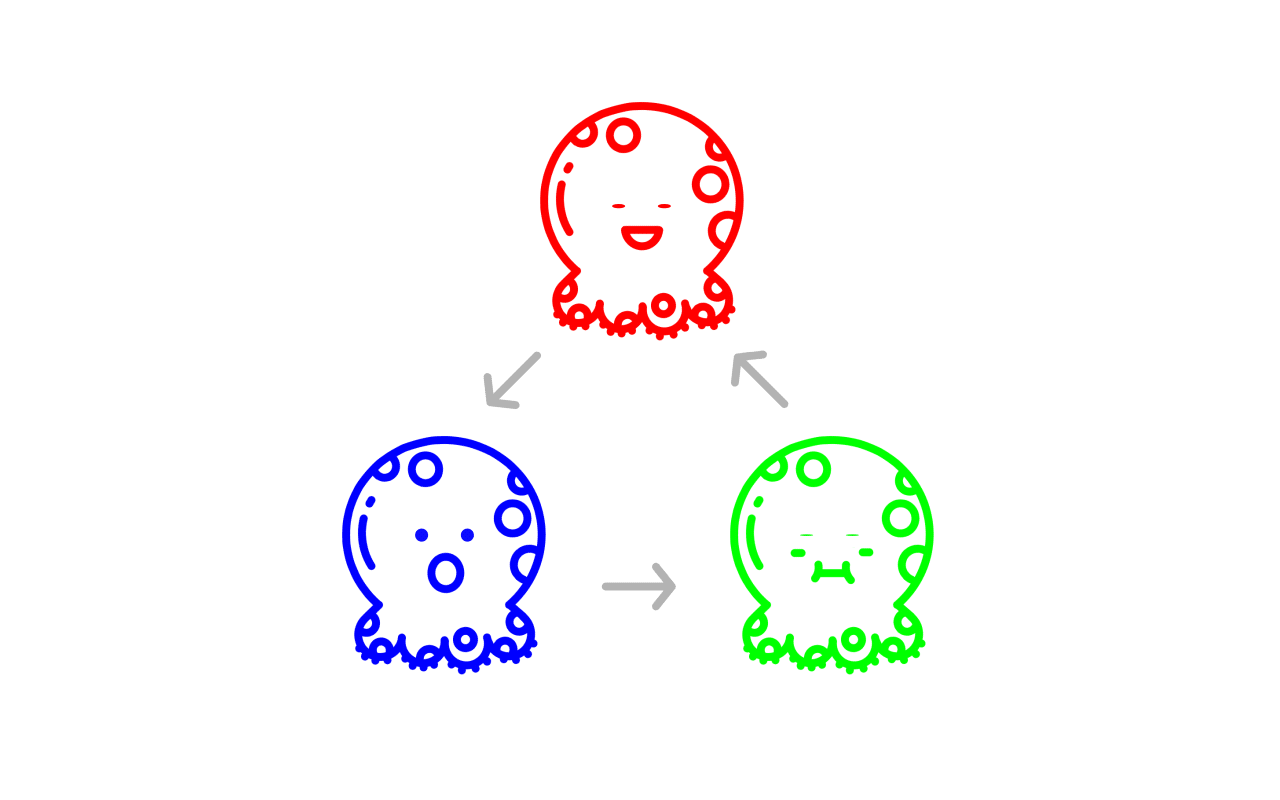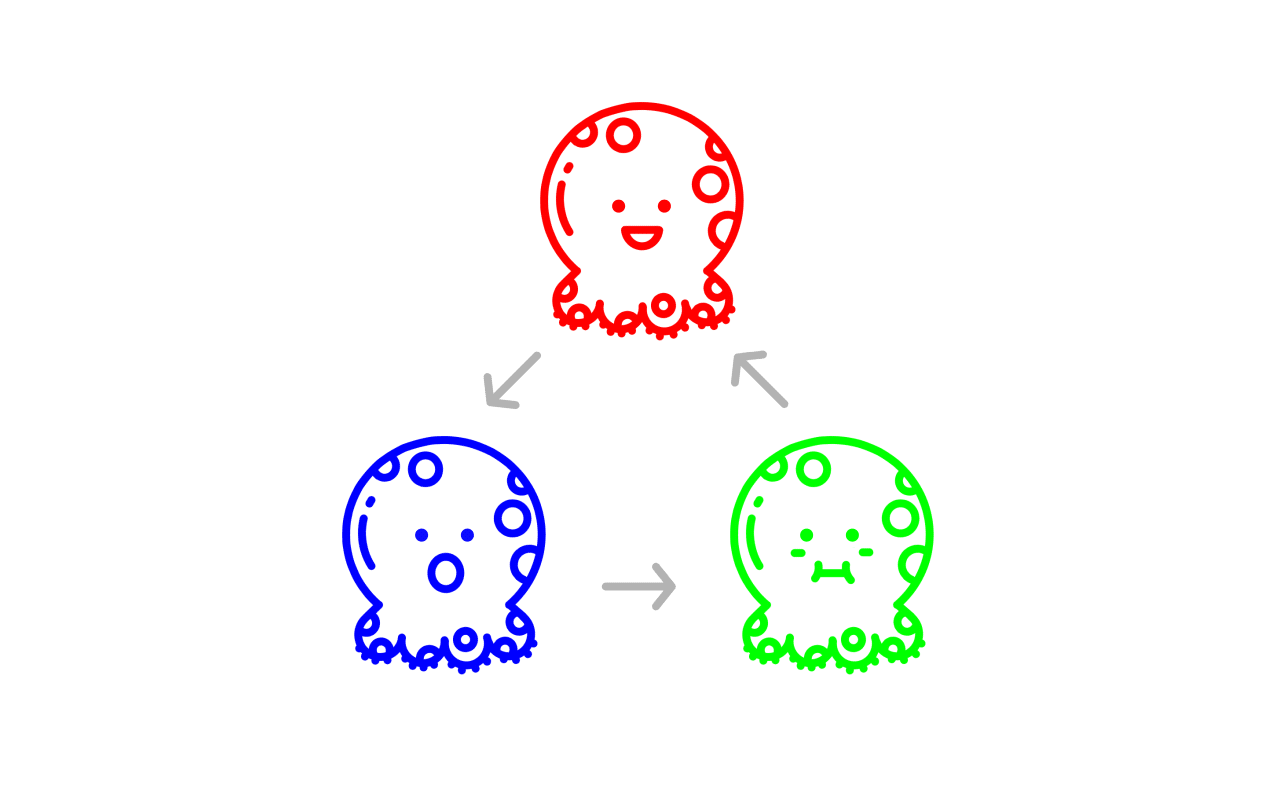
我们用代码制定了这个简单的食物链规则之后,便放手让这个“RGB”系统自主地去运作,不再参与其中。你会发现它演变成了一个很有意思的动态影像,这是我们在指定那个食物链规则的时候很难预测到的:RGB 3种生物按照食物链规则互相吞噬,生成了一种螺旋式的生生不息的群态。

反应扩散算法(Reaction-Diffusion)也可以算是非单一物种参与的活系统的一个经典例子。在反应扩散算法里,设定了两种互相作用的化学物质(生物)—— A和B,并规定了关于A和B的三条生存法则:
第一,A生物会以固定的速率增加并添加到系统之中。

第二,2个B生物会把1个A生物转换成B生物(可以理解为2个B生物吃了A生物,并繁衍出1个B的后代)。
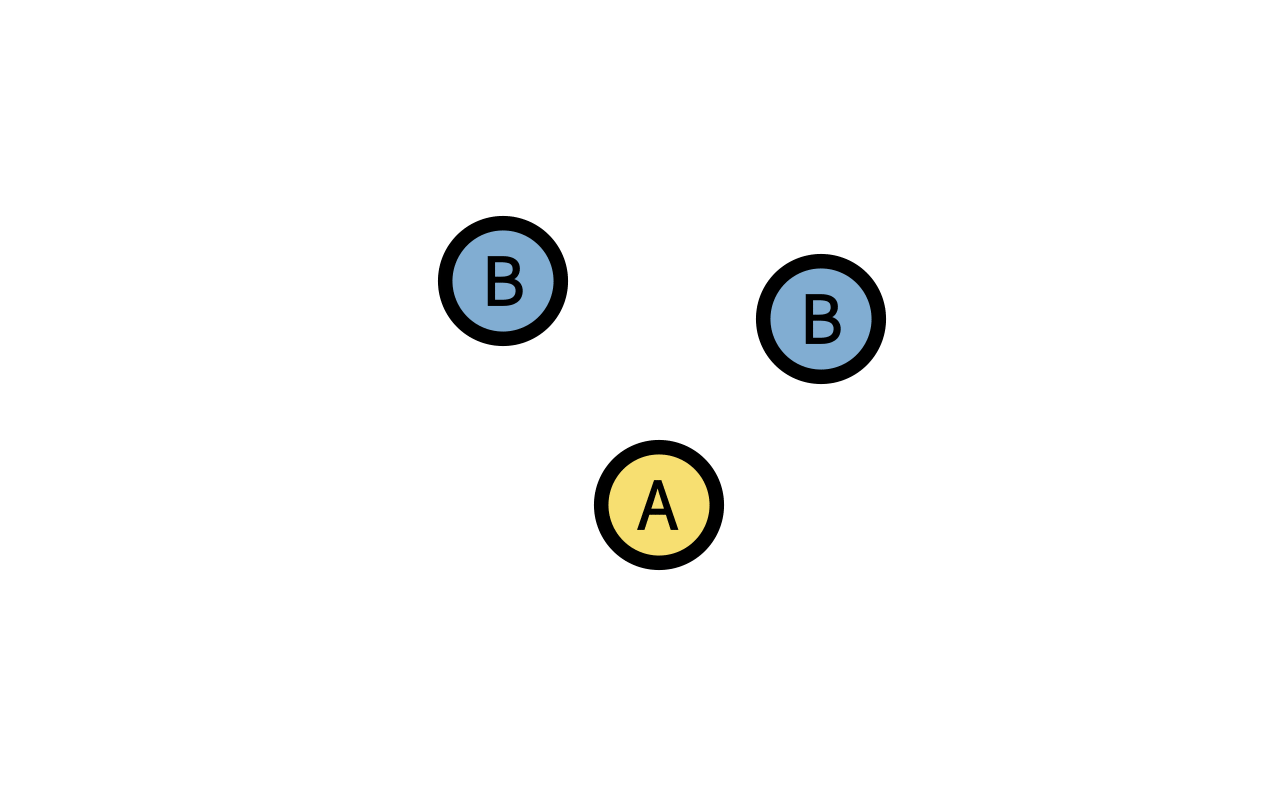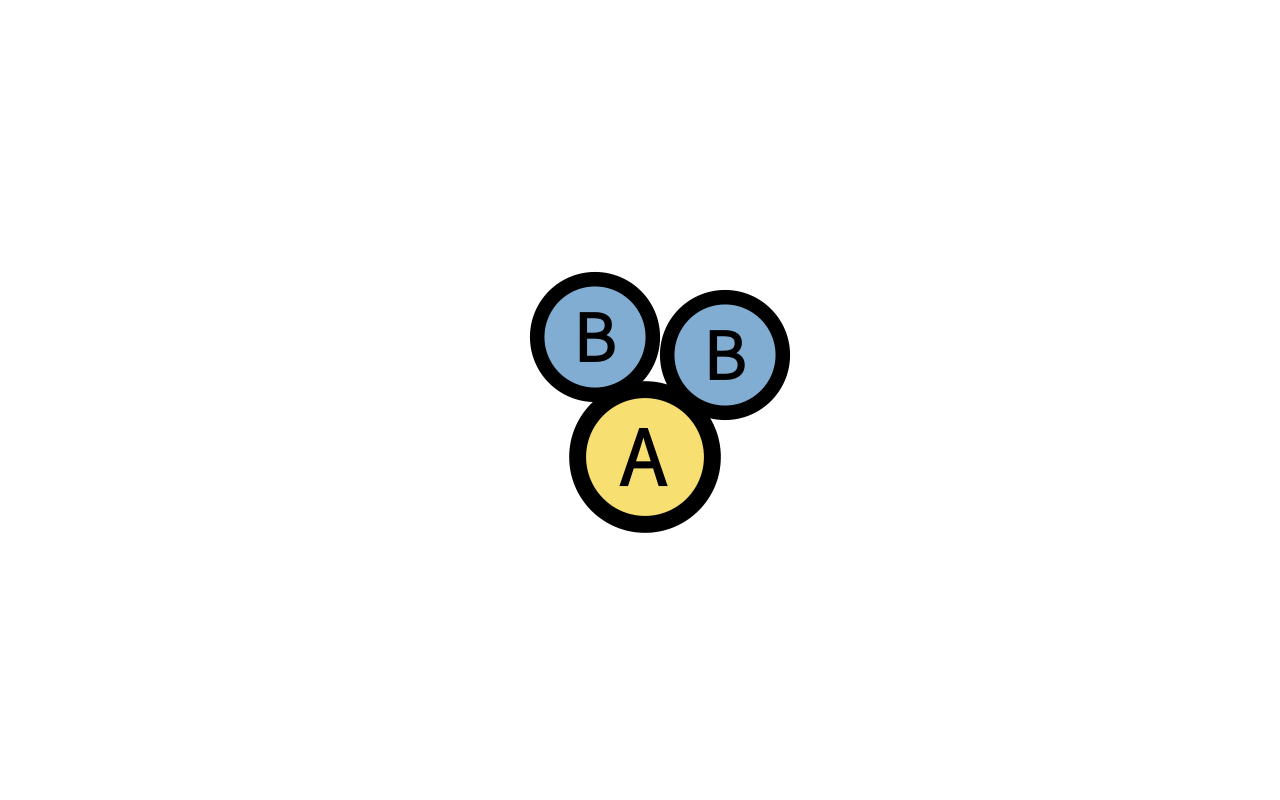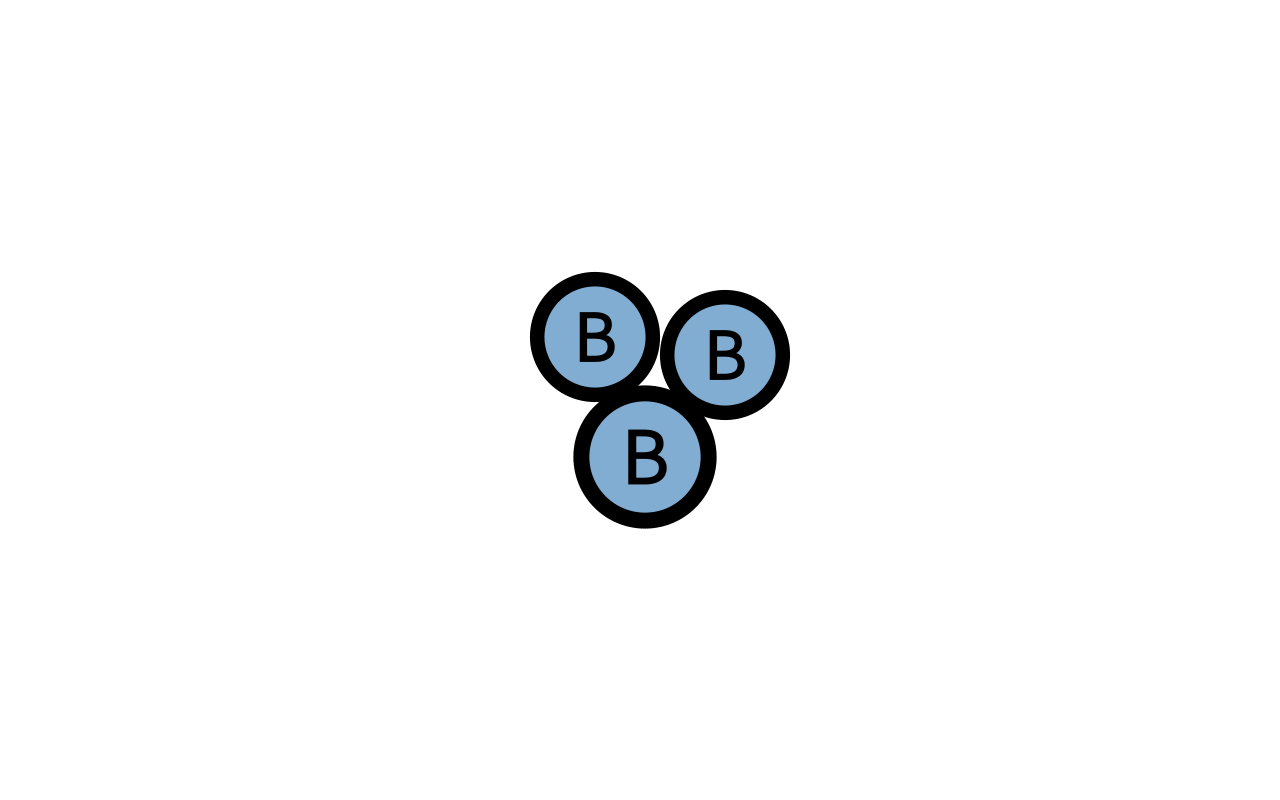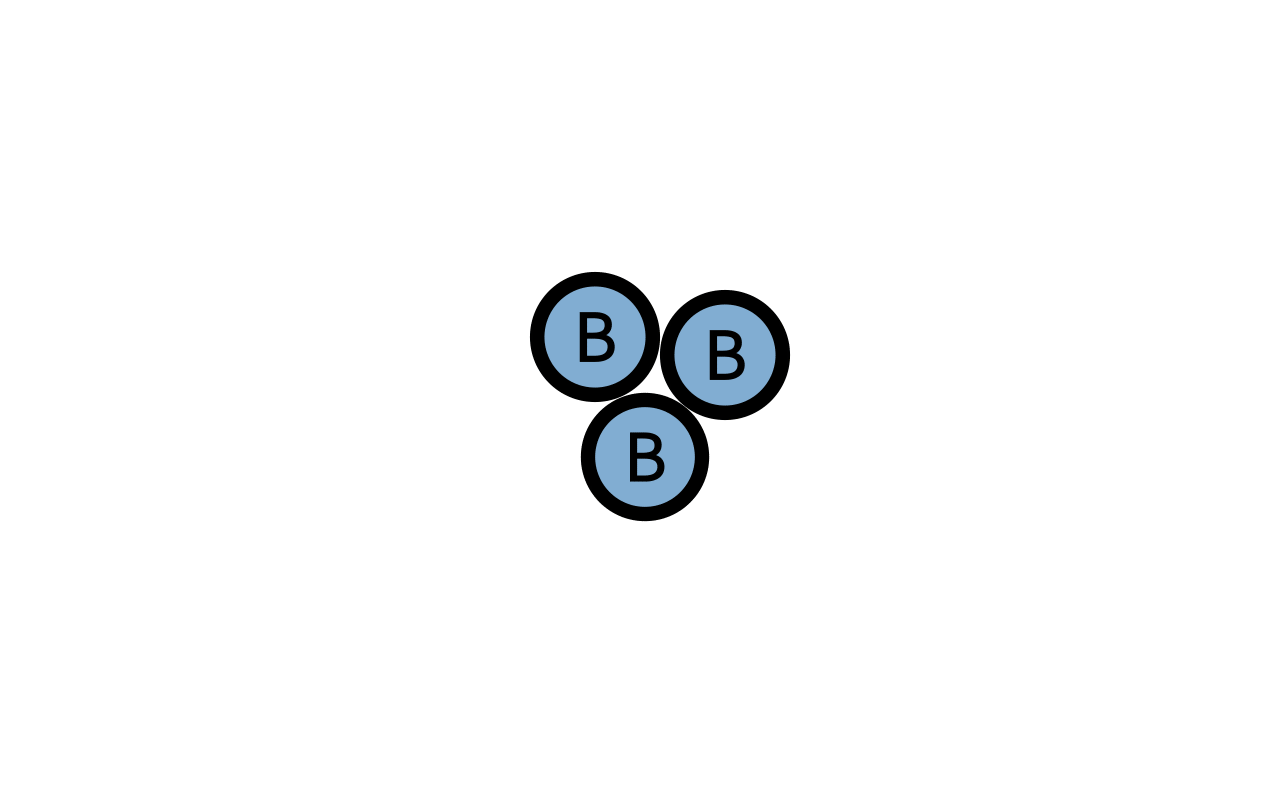
第三,B生物会以固定的速率死去。
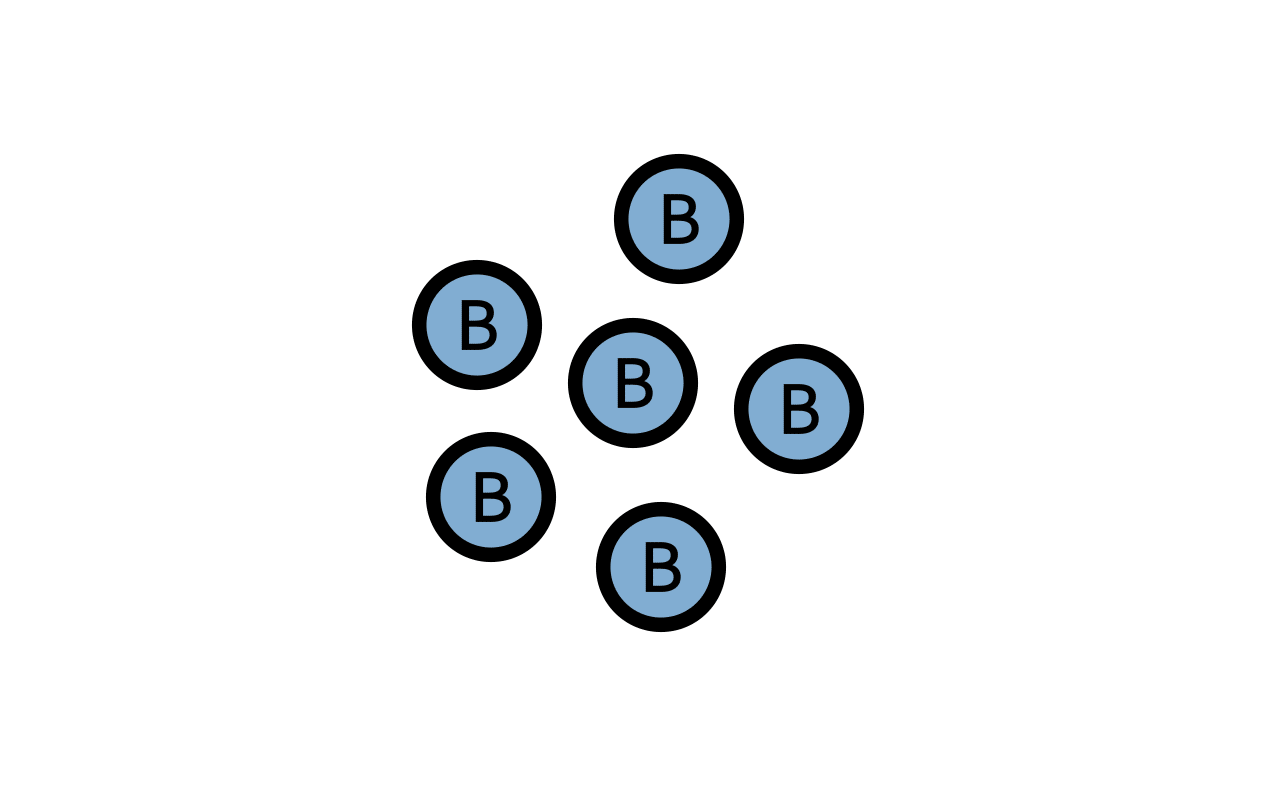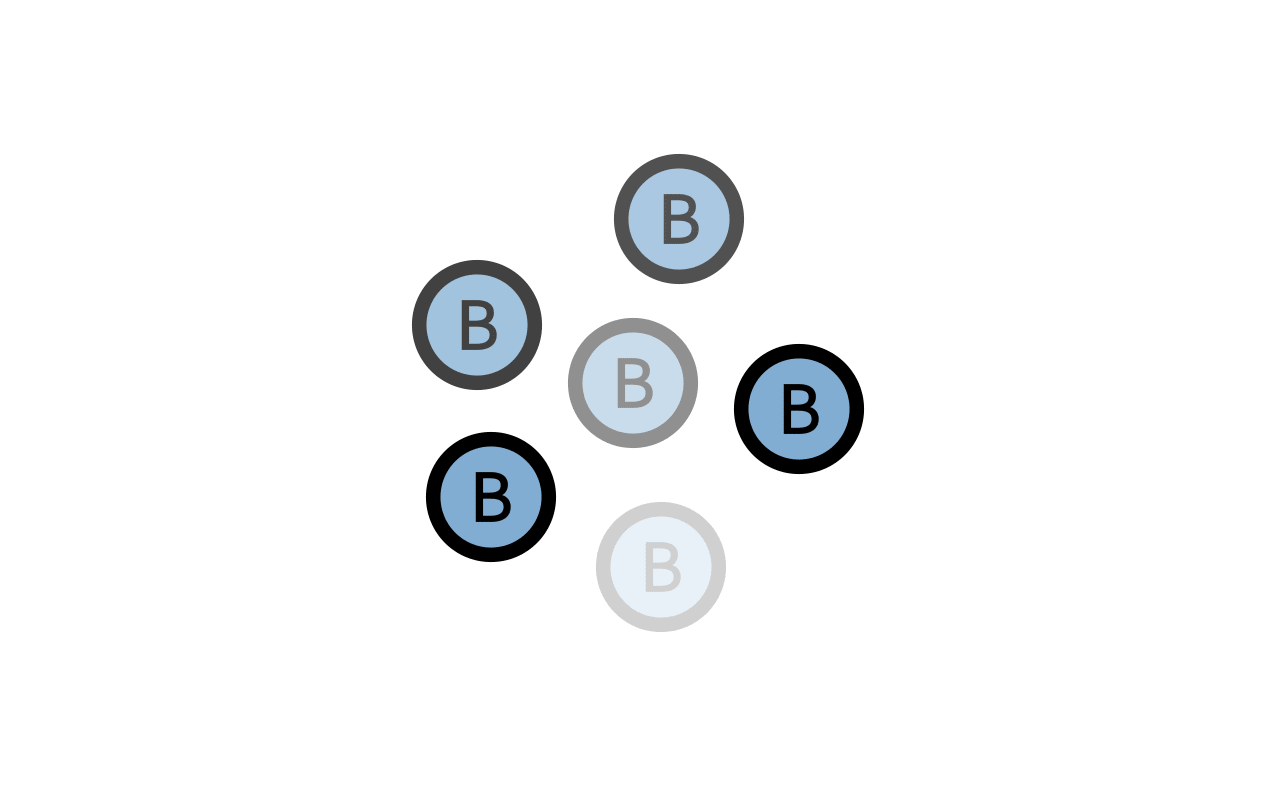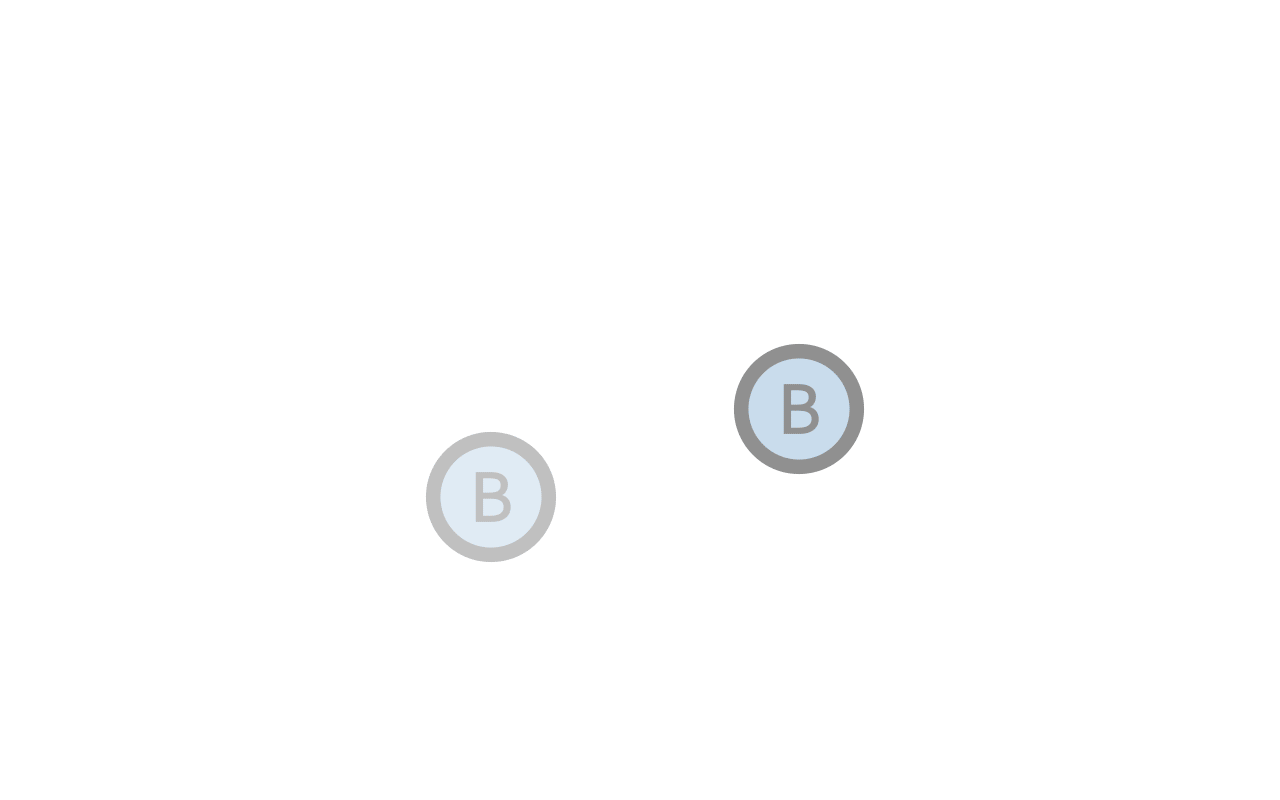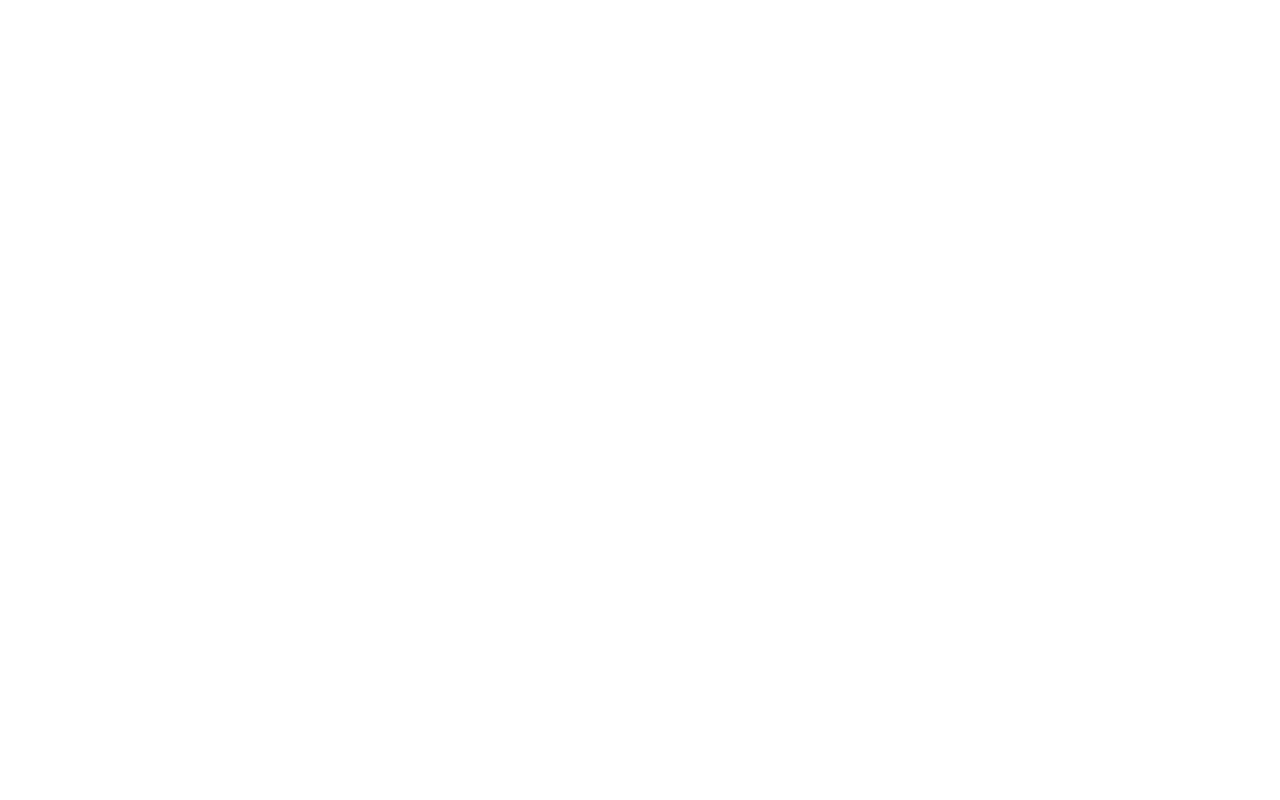
根据这三条简单的规则,我们就可以让系统自动去演变了,在生物A和B的相互作用下,系统呈现出了惊奇且复杂的形态。我们可以通过调整A的增加速率以及B的死亡速率,来让系统演变成不同的复杂形态。
Video from Karl Sims
Video from Karl Sims
让我们再看回文章开头史蒂芬·沃尔夫勒姆说过的话。
“在计算的宇宙中凭借简单规则可以出现一些非常复杂的现象。”
这句话背后蕴含的含义,远远超过本文所提及的内容。甚至于本文只讨论了表象,却没深入探究活系统是在什么时候开始涌现出更高级更复杂的群态?少数个体组成的群体是不会涌现出更高级更复杂的特性。一个“合格”的活系统需要有足够多的个体,来提供足够多的个体之间的相互作用;同时它也需要足够长的时间才能出现涌现现象,正如凯文·凯利所说的—— “有机的复杂性需要有机的时间。”
在失控的系统中,简单的运算规则生成复杂的艺术形态,这是一个很有趣的课题,本文简单地讨论了表象,仅作抛砖引玉。






































